Các kiến thức trong toán học là vô hạn, đặc biệt là định nghĩa về số chính phương. . Vậy số chính phương là gì, và nó có ý nghĩa ra sao? Bài viết này sẽ giúp bạn hiểu rõ hơn về định nghĩa, tính chất, và cách xác định một số chính phương, đồng thời cung cấp một số ví dụ minh họa dễ hiểu.
|
Số chính phương là gì
Số chính phương là một số nguyên có thể được viết dưới dạng bình phương của một số nguyên khác. Nói cách khác, một số n là số chính phương nếu và chỉ nếu tồn tại một số nguyên k sao cho n=k^2
Ví dụ:
- 1 là số chính phương vì 1=1^2
- 4 là số chính phương vì 4=2^2
- 9 là số chính phương vì 9=3^2
- 16 là số chính phương vì 16=4^2
Tóm lại, số chính phương là các số được tạo ra bằng cách bình phương một số nguyên.
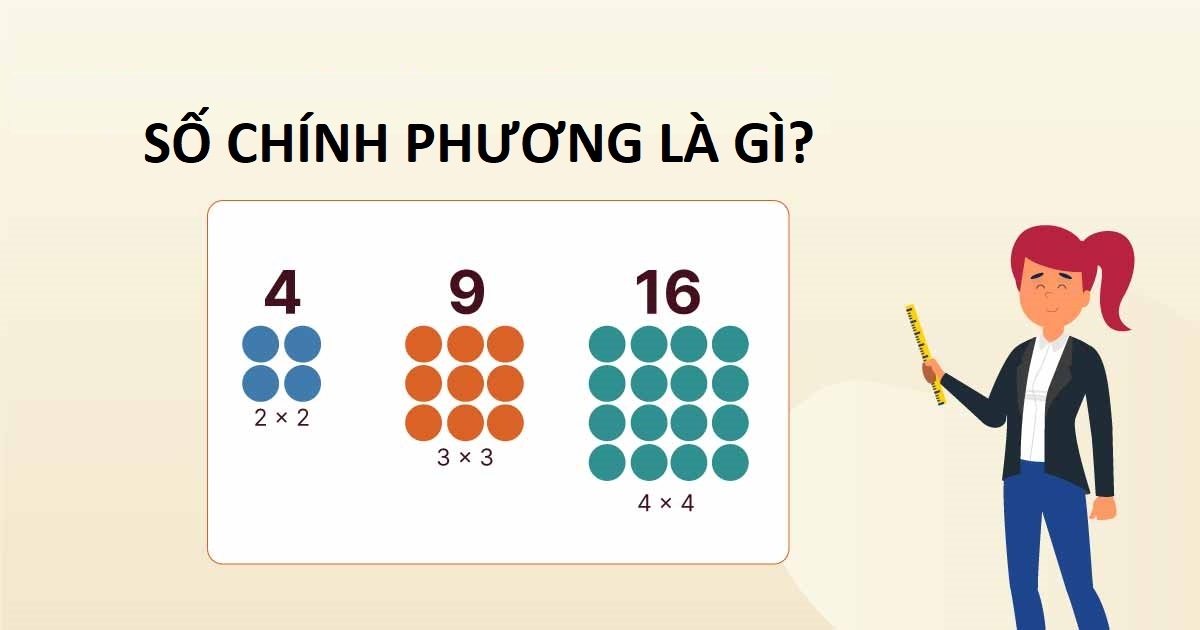
Định nghĩa số chính phươngĐể kiểm tra xem một số có phải là số chính phương hay không, bạn có thể thực hiện các bước sau:
- Tính căn bậc hai: Tính căn bậc hai của số đó. Giả sử số cần kiểm tra là n.
- Kiểm tra kết quả: Xem xét kết quả của căn bậc hai. Nếu căn bậc hai của n là một số nguyên, thì n là số chính phương. Nếu không, thì nó không phải là số chính phương.
- Cụ thể, đây là quy trình chi tiết:
- Tính căn bậc hai: Tính giá trị căn bậc 2 của n. Ví dụ, nếu n=36, tính căn bậc hai của 36 = 6
- Kiểm tra tính nguyên: Kiểm tra xem kết quả có phải là số nguyên không. Trong ví dụ trên, 6 là số nguyên, vì vậy 36 là số chính phương.
- Kiểm tra lại: Để chắc chắn, bạn có thể bình phương kết quả để xem có trả về số ban đầu không. Trong ví dụ trên, 6^2=36, điều này xác nhận rằng 36 là số chính phương.
Nếu bạn đang làm việc với một số lớn hoặc không chắc chắn, bạn có thể sử dụng các công cụ hoặc hàm tính toán trên máy tính hoặc phần mềm toán học để thực hiện các bước này.
Ví dụ
- Để kiểm tra xem 49 có phải là số chính phương không:
- Tính căn bậc hai của 49: căn bậc hai 49 = 7
- Kiểm tra xem 7 có phải là số nguyên không: Đúng.
- Bình phương 7: 7^2=49. Vì vậy, 49 là số chính phương.
- Để kiểm tra xem 50 có phải là số chính phương không:
- Tính căn bậc hai của 50: căn bậc hai 50≈7.07.
- 7.07 không phải là số nguyên, vì vậy 50 không phải là số chính phương.
Hy vọng điều này giúp bạn kiểm tra một số xem có phải là số chính phương hay không!

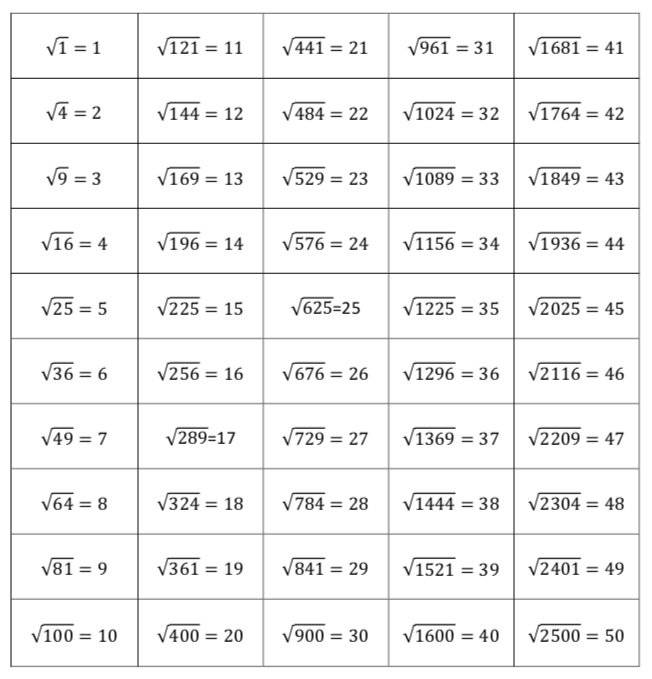
Cách kiểm tra 1 số là số chính phươngCác số chính phương đầu tiên là những số nguyên dương có thể được viết dưới dạng bình phương của một số nguyên. Dưới đây là danh sách các số chính phương đầu tiên:
- 1 (vì 1=1^2)
- 4 (vì 4=2^2)
- 9 (vì 9=3^2)
- 16 (vì 16=4^2)
- 25 (vì 25=5^2)
- 36 (vì 36=6^2)
- 49 (vì 49=7^2)
- 64 (vì 64=8^2)
- 81 (vì 81=9^2)
- 100 (vì 100=10^2)
Dãy số chính phương tiếp tục theo cách này: n^2, với n là một số nguyên dương. Sau 100, các số chính phương tiếp theo sẽ là 121 (11^2), 144 (12^2), 169 (13^2), và cứ tiếp tục như vậy.
Số chính phương nhỏ nhấtCông thức tổng quát để tính số chính phương là:n^2
Trong đó:
- n là một số nguyên dương.
Giải thích:
- Số chính phương là một số nguyên có thể được viết dưới dạng bình phương của một số nguyên. Vì vậy, bất kỳ số nào có dạng n^2, với n là một số nguyên, đều là một số chính phương.
Ví dụ:
- Nếu n=3, thì số chính phương là 3^2=9
- Nếu n=7, thì số chính phương là 7^2=49
- Nếu n=12, thì số chính phương là 12^2=144.
Như vậy, để tìm một số chính phương, bạn chỉ cần bình phương một số nguyên.
Một số ví dụ về số chính phươngSố chính phương xuất hiện trong nhiều ví dụ thực tế từ các lĩnh vực khác nhau như toán học, hình học, kiến trúc, và các tình huống trong đời sống hằng ngày. Dưới đây là một số ví dụ thực tế về số chính phương:
Diện tích của hình vuông:
- Trong hình học, diện tích của một hình vuông được tính bằng bình phương của độ dài cạnh. Ví dụ, nếu một hình vuông có cạnh dài 5 đơn vị, thì diện tích của nó là 5^2 = 25 đơn vị vuông. Do đó, diện tích của hình vuông luôn là một số chính phương.
Sắp xếp đồ vật thành hình vuông:
- Khi sắp xếp các đồ vật (ví dụ như viên gạch, viên bi, hay ô vuông) thành một hình vuông, tổng số đồ vật sẽ là một số chính phương. Ví dụ, nếu bạn có 16 viên bi và sắp xếp chúng thành một hình vuông, bạn sẽ có 4 viên ở mỗi hàng và mỗi cột (vì 4^2 = 16).
Bảng cửu chương:
- Bảng cửu chương cung cấp nhiều ví dụ về số chính phương khi bạn nhân một số với chính nó. Ví dụ, trong bảng cửu chương:
- 2×2=4(4 là số chính phương)
- 3×3=9(9 là số chính phương)
- 5×5=25(25 là số chính phương)
Số bước trong việc tạo lưới hoặc phân bố đều:
- Trong việc tạo lưới (ví dụ như trồng cây hay xếp ghế theo hình vuông trong một sự kiện), tổng số cây hoặc ghế sẽ là một số chính phương nếu bạn xếp chúng thành hình vuông. Ví dụ, nếu bạn có 9 cây và muốn xếp chúng thành một lưới hình vuông, bạn sẽ xếp 3 hàng và 3 cột (vì 3^2 = 9).
Lập phương Rubik:
- Lập phương Rubik 3x3x3 có 9 ô vuông trên mỗi mặt, và 9 là một số chính phương (vì 3^2 = 9).
Kiến trúc và nghệ thuật:
- Trong kiến trúc, việc sử dụng các ô vuông đều trong thiết kế thường dẫn đến tổng diện tích hay số lượng các ô vuông là một số chính phương. Ví dụ, một bức tranh được phân thành 25 ô vuông nhỏ thì tổng số ô là 5^2 = 25.
Chơi trò chơi xếp hình:
- Trong các trò chơi xếp hình hoặc xếp đồ vật thành hình vuông, số lượng ô vuông hoặc mảnh ghép cần sử dụng để tạo ra một hình vuông lớn hoàn chỉnh thường là một số chính phương. Ví dụ, nếu bạn có 49 mảnh ghép, bạn có thể xếp chúng thành một hình vuông 7x7 (vì 7^2 = 49).
Màn hình và độ phân giải:
- Một số màn hình có độ phân giải được thể hiện bằng số lượng điểm ảnh là số chính phương. Ví dụ, màn hình có độ phân giải 1024x1024 là một ví dụ, với tổng số điểm ảnh trên chiều dài và chiều rộng đều là số chính phương (vì 1024 là một số chính phương).
Những ví dụ trên cho thấy số chính phương không chỉ là một khái niệm toán học mà còn xuất hiện nhiều trong thực tế, từ hình học đến đời sống thường ngày.
Như vậy là bạn đã hiểu rõ hơn về số chính phương và cũng đã làm quen với một số dạng bài tập liên quan đến chủ đề này. Hy vọng rằng bạn đã có cái nhìn tổng quan về số chính phương là gì. Chúc bạn học được nhiều kiến thức hữu ích từ bài viết này!
|
|
|