Công thức cấp số cộng
Định nghĩa
Cấp số cộng là một dãy số mà trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi. Số không đổi này được gọi là công sai của cấp số cộng và thường được kí hiệu là d.
Ví dụ:
Dãy số 3, 7, 11, 15,... là cấp số cộng với công sai d = 4.
Dãy số 10, 7, 4, 1,... cũng là cấp số cộng nhưng có công sai d = -3 (công sai âm).
Những điều thú vị về cấp số cộng
Cấp số cộng có thể tăng hoặc giảm: Tùy thuộc vào giá trị của công sai d, cấp số cộng có thể tăng dần (d > 0), giảm dần (d < 0) hoặc là một dãy số không đổi (d = 0).
Ứng dụng trong đời sống: Cấp số cộng được sử dụng trong nhiều lĩnh vực như tài chính, kỹ thuật, khoa học tự nhiên,...
Có nhiều bài toán hay và thú vị liên quan đến cấp số cộng: Việc giải các bài toán về cấp số cộng không chỉ giúp bạn rèn luyện kỹ năng tính toán mà còn giúp bạn phát triển tư duy logic.
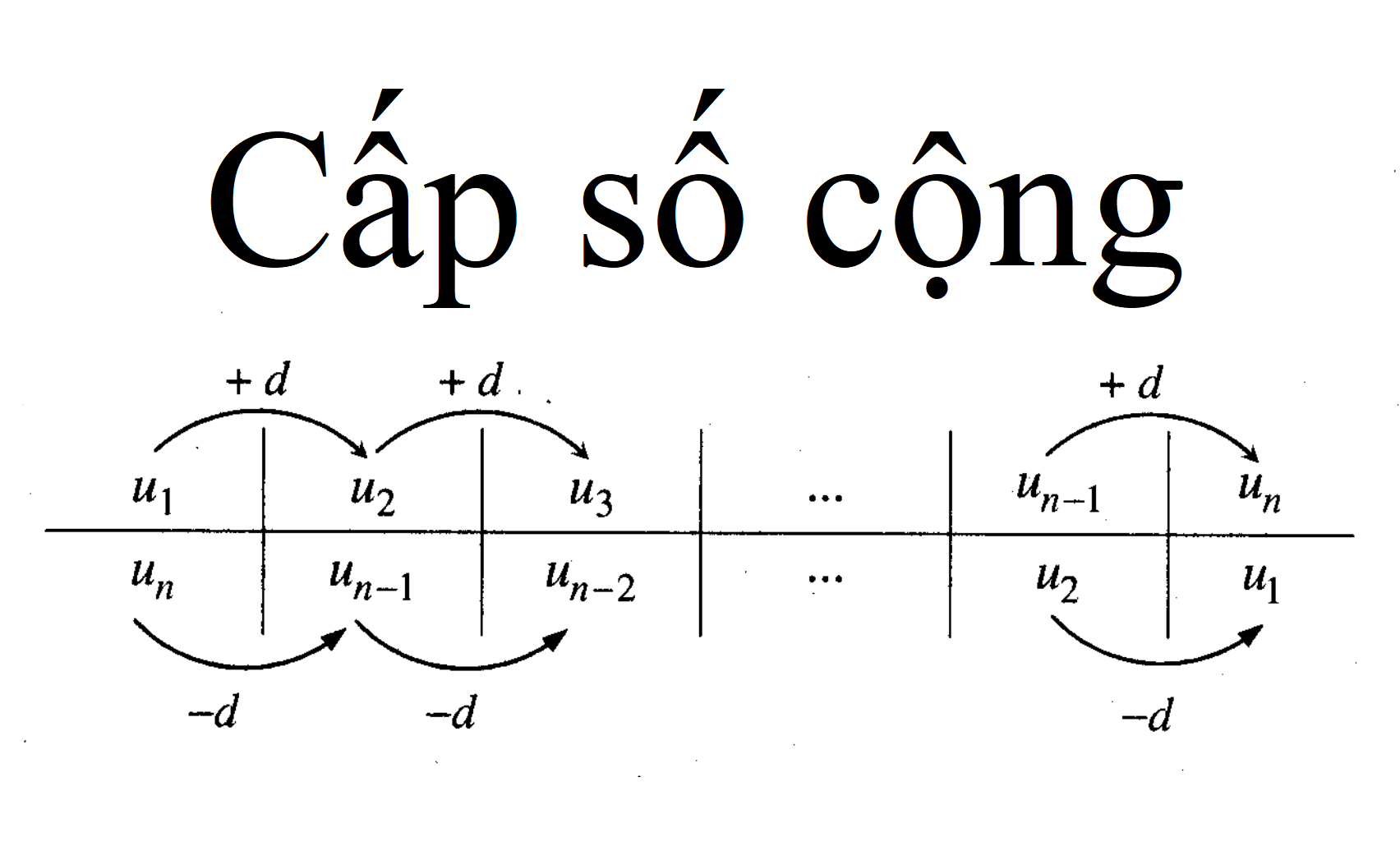
Minh họa cấp số cộngSố hạng tổng quát
Mỗi số hạng trong cấp số cộng có thể tính được bằng công thức:
Un = U1 + (n - 1)d Trong đó:
Un: Số hạng thứ n
U1: Số hạng đầu tiên
n: Vị trí của số hạng
d: Công sai
Tổng n số hạng đầu
Tổng của n số hạng đầu tiên của cấp số cộng được tính bằng công thức:
Sn = n/2 * [2U1 + (n - 1)d] hoặc
Sn = n/2 * (U1 + Un)
Tính chất trung bình cộng
Mỗi số hạng (trừ số hạng đầu và cuối) bằng trung bình cộng của hai số hạng đứng kề nó.
Ví dụ minh họa
Dãy số 2, 4, 6, 8, ... là cấp số cộng với U1 = 2 và d = 2.
Để tính số hạng thứ 10 của dãy số trên, ta áp dụng công thức:
U10 = 2 + (10 - 1) * 2 = 20.
Để tính tổng 10 số hạng đầu tiên, ta áp dụng công thức:
S10 = 10/2 * (2 + 20) = 110.
Ứng dụng của cấp số cộng
Cấp số cộng có rất nhiều ứng dụng trong cuộc sống và các lĩnh vực khác nhau như:
Vật lý: Mô tả chuyển động đều, tính quãng đường, vận tốc.
Kinh tế: Tính lãi suất đơn giản, dự báo doanh thu.
Xây dựng: Tính số lượng gạch, tính toán kích thước.

Tính chất cấp số cộng có nhiều điểm đặc biệt thú vịCông thức tính số hạng tổng quát
Ý nghĩa: Cho phép ta tính giá trị của bất kỳ số hạng nào trong cấp số cộng khi biết số hạng đầu và công sai.
Công thức: un = u1 + (n-1)d
un: Số hạng thứ n
u1: Số hạng đầu
n: Vị trí của số hạng
d: Công sai
Công thức tính tổng n số hạng đầu
Ý nghĩa: Giúp ta tính nhanh tổng của một đoạn bất kỳ các số hạng trong cấp số cộng.
Công thức: Sn = n[2u1 + (n-1)d]/2
Sn: Tổng n số hạng đầu
u1: Số hạng đầu
n: Số lượng số hạng
d: Công sai
Các công thức liên quan
Tính công sai: d = un - un-1
Tính số hạng đầu: u1 = un - (n-1)d

Một số công thức về cấp số cộng đơn giảnNhận biết cấp số cộng
Xác định xem một dãy số cho trước có phải là cấp số cộng hay không.
Tìm công sai của cấp số cộng.
Tìm số hạng tổng quát
Dựa vào số hạng đầu và công sai, viết công thức tính số hạng thứ n của cấp số cộng.
Tính tổng n số hạng đầu
Sử dụng công thức tổng quát để tính tổng của một đoạn các số hạng liên tiếp trong cấp số cộng.
Bài toán liên quan đến các điều kiện cho trước
Tìm các số hạng của cấp số cộng khi biết một số điều kiện về tổng, tích, hoặc các mối quan hệ giữa các số hạng.
Ứng dụng cấp số cộng vào bài toán thực tế
Giải quyết các bài toán liên quan đến lãi kép, giảm giá, hoặc các vấn đề liên quan đến sự tăng trưởng đều đặn.
Tại sao bạn nên học về cấp số cộng?
Rèn luyện tư duy logic: Giải các bài tập cấp số cộng giúp bạn rèn luyện khả năng suy luận, phân tích và tổng hợp thông tin.
Nâng cao kỹ năng giải toán: Cấp số cộng cung cấp cho bạn một công cụ mạnh mẽ để giải quyết các bài toán phức tạp hơn.
Mở rộng kiến thức: Hiểu về cấp số cộng sẽ giúp bạn khám phá nhiều lĩnh vực toán học khác một cách sâu sắc hơn.
Ứng dụng của cấp số cộng trong thực tế
Kinh tế:
Tăng trưởng kinh tế: Tốc độ tăng trưởng GDP của một quốc gia trong nhiều năm liền thường tạo thành một cấp số cộng.
Lãi suất: Lãi đơn tính theo cấp số cộng.
Giá cả: Giá cả hàng hóa có thể tăng dần theo cấp số cộng trong một khoảng thời gian nhất định.
Vật lý:
Chuyển động thẳng đều: Quãng đường đi được của một vật chuyển động thẳng đều trong những khoảng thời gian bằng nhau tạo thành một cấp số cộng.
Dao động điều hòa: Biên độ dao động của một vật dao động điều hòa giảm dần theo cấp số cộng.
Sinh học:
Sự sinh trưởng của vi khuẩn: Trong điều kiện thuận lợi, số lượng vi khuẩn trong một môi trường nuôi cấy có thể tăng lên theo cấp số cộng.
Quá trình phân chia tế bào: Số lượng tế bào con sau mỗi lần phân chia tăng lên theo cấp số cộng.
Xã hội:
Dân số: Dân số của một quốc gia có thể tăng lên theo cấp số cộng trong một khoảng thời gian nhất định.
Lương: Mức lương của một người có thể tăng dần theo cấp số cộng qua các năm.
Trên đây là các thông tin về chủ đề công thức cấp số cộng. Cấp số cộng là kiến thức rất quan trọng trong chương trình học phổ thông, nó được áp dụng vào rất nhiều dạng bài tập cũng như ứng dụng vào thực tế rất đa dạng. Hi vọng với những thông tin trên đây, quý bạn đọc đã có cho mình thông tin hữu ích.