Số chính phương là gì

1. Người phát minh ra số chính phương là ai? 

Số chính phương là gì? Số chính phương (hay còn gọi là số hình vuông) không phải là một phát minh của một cá nhân cụ thể, mà là một khái niệm toán học tự nhiên đã được phát hiện và sử dụng từ rất sớm trong lịch sử nhân loại.

Số chính phương là gì? Số chính phương là số được tạo ra bằng cách bình phương một số nguyên. Ví dụ, 1, 4, 9, 16, và 25 là các số chính phương vì chúng là bình phương của 1, 2, 3, 4 và 5.

Tìm hiểu về số chính phương

Người ta đã biết đến số chính phương từ thời cổ đại, đặc biệt là trong các nền văn minh như Ai Cập, Babylon và Hy Lạp cổ đại. Các nhà toán học Hy Lạp như Pythagoras và Euclid đã nghiên cứu sâu về các tính chất của số chính phương trong hình học và lý thuyết số.

Vì vậy, số chính phương không có người phát minh cụ thể mà là một khái niệm đã được khám phá và nghiên cứu qua nhiều thế hệ trong lịch sử toán học.
Tham khảo: Định lý pytago

2. Vì sao số chính phương lại xuất hiện?

Số chính phương xuất hiện tự nhiên trong toán học từ nhu cầu mô tả và giải quyết các vấn đề liên quan đến diện tích, hình học, và mối quan hệ giữa các con số. Dưới đây là một số lý do vì sao số chính phương lại xuất hiện:

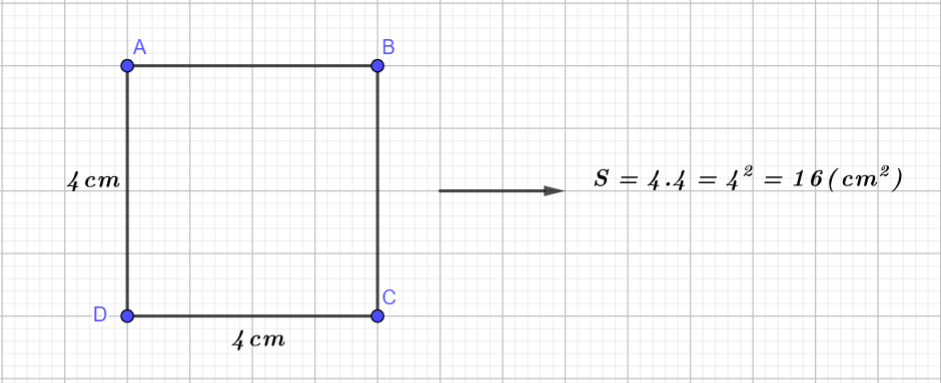
• Liên hệ với diện tích hình vuông: Số chính phương ban đầu xuất phát từ hình học, khi người ta tính diện tích của một hình vuông. Nếu một hình vuông có cạnh dài 𝑛, thì diện tích của nó là 𝑛^2. Vì vậy, số chính phương biểu thị diện tích của một hình vuông với cạnh là một số nguyên.

• Khám phá trong số học: Khi con người bắt đầu nghiên cứu các mối quan hệ giữa các số, họ phát hiện ra rằng việc nhân một số với chính nó (tức là bình phương một số) mang lại những kết quả đặc biệt. Ví dụ, họ nhận thấy rằng các số như 4, 9, 16 có mối liên hệ với hình học và có những tính chất đặc biệt trong lý thuyết số.

• Ứng dụng trong hình học và đo lường: Trong hình học cổ đại, các nhà toán học như Euclid và Pythagoras đã sử dụng số chính phương để giải quyết các bài toán liên quan đến đo lường và hình học. Chẳng hạn, định lý Pythagoras, một trong những định lý cơ bản của hình học, có liên quan đến bình phương của các cạnh trong tam giác vuông.

• Phát triển lý thuyết số: Số chính phương cũng có vai trò quan trọng trong lý thuyết số, một nhánh của toán học nghiên cứu về các tính chất và mối quan hệ giữa các số nguyên. Các nhà toán học nghiên cứu số chính phương để hiểu rõ hơn về cấu trúc của các con số và cách chúng tương tác với nhau trong các phép toán.

• Ứng dụng trong giải phương trình: Số chính phương còn xuất hiện tự nhiên trong các phương trình bậc hai (có dạng 𝑎𝑥^2 + 𝑏𝑥 + 𝑐 = 0 và các phương trình khác liên quan đến bình phương của một số. Đây là một loại phương trình phổ biến trong toán học và khoa học.

Tóm lại, số chính phương xuất hiện vì nhu cầu tính toán và hiểu biết về hình học, đo lường, và lý thuyết số. Chúng không chỉ mang ý nghĩa toán học mà còn có ứng dụng thực tế trong cuộc sống, như việc tính diện tích hay giải quyết các bài toán trong khoa học và kỹ thuật

3. Bài tập về số chính phương:

Bài tập chứng minh số chính phương

4. Dấu hiệu nhận biết số chính phương là gì?

Để nhận biết một số có phải là số chính phương hay không (tức là số có thể được viết dưới dạng bình phương của một số nguyên), có một số dấu hiệu quan trọng như sau:

1. Dấu hiệu về chữ số tận cùng:

Số chính phương chỉ có thể có các chữ số tận cùng (chữ số hàng đơn vị) là một trong các chữ số sau:

0, 1, 4, 5, 6, hoặc 9.

Ví dụ:

16 có tận cùng là 6 (số chính phương của 4).

25 có tận cùng là 5 (số chính phương của 5).

Nếu số có chữ số tận cùng là 2, 3, 7 hoặc 8, thì chắc chắn không phải số chính phương.

2. Số lượng chữ số tận cùng bằng 0:

Nếu một số chính phương có chữ số tận cùng là 0, thì số đó phải có số lượng chữ số 0 ở cuối là số chẵn. Ví dụ:

100 = 10^2 (có hai chữ số 0).

1600 = 40^2 (có hai chữ số 0).

Nếu có số lẻ các chữ số 0 ở cuối, số đó không phải là số chính phương.

3. Tính chất tổng chữ số:

Nếu tổng các chữ số của một số là bội số của 3 (chia hết cho 3), thì số đó có thể là số chính phương. Tuy nhiên, dấu hiệu này chỉ là điều kiện cần và không phải luôn đúng cho tất cả các số.

Ví dụ:

81 là số chính phương của 9, và tổng các chữ số của 81 là 

8+1=9, chia hết cho 3.

4. Căn bậc hai là số nguyên:

Dấu hiệu chính xác nhất để kiểm tra một số có phải là số chính phương hay không là tính căn bậc hai của nó. Nếu căn bậc hai là một số nguyên, thì số đó là số chính phương.

Ví dụ

Ví dụ:

Căn bậc hai của 25 là 5 (số nguyên) ⇒ 25 là số chính phương.

Căn bậc hai của 20 là 4,47 (không phải số nguyên) ⇒ 20 không phải số chính phương.

5. Tích các ước số lẻ:

Số chính phương có tổng số ước là số lẻ. Ví dụ:

16 có các ước là 1, 2, 4, 8, 16 (tổng cộng 5 ước, là số lẻ) ⇒ 16 là số chính phương.

12 có các ước là 1, 2, 3, 4, 6, 12 (tổng cộng 6 ước, là số chẵn) ⇒ 12 không phải là số chính phương.

6. Chia cho 4 và 3:

Số chính phương khi chia cho 4 chỉ có thể dư 0 hoặc 1.

Khi chia cho 3, số chính phương chỉ có thể dư 0 hoặc 1.

Ví dụ:

16÷4=4 (dư 0), vậy 16 có thể là số chính phương.

10÷4=2,5 (dư 2), vậy 10 không phải là số chính phương.

Tóm lại, để nhận biết một số có phải là số chính phương hay không, có thể dùng các dấu hiệu như chữ số tận cùng, số lượng chữ số 0 ở cuối, và đặc biệt là tính căn bậc hai của số đó. Tuy nhiên, tính căn bậc hai là cách chắc chắn nhất để kiểm tra.