Số chính phương là gì
Bạn đã bao giờ tự hỏi tại sao số 4, 9, 16 lại đặc biệt? Chúng không chỉ là những con số đơn thuần mà còn ẩn chứa một quy luật thú vị trong toán học. Đó chính là số chính phương.
Số chính phương là gì?
Số chính phương là một số tự nhiên mà khi ta lấy căn bậc hai của nó, kết quả cũng là một số tự nhiên. Nói cách khác, số chính phương là bình phương của số nguyên.
Ví dụ:
4 là số chính phương vì 4 = 2²
9 là số chính phương vì 9 = 3²
16 là số chính phương vì 16 = 4²
Tại sao số chính phương lại đặc biệt?
Hình học: Số chính phương có thể là diện tích của 1 hình vuông có cạnh là 1 số tự nhiên. Ví dụ, một hình vuông có cạnh dài 3 đơn vị sẽ có diện tích là 3 x 3 = 9 đơn vị diện tích.
Ứng dụng: Số chính phương có nhiều ứng dụng trong các lĩnh vực khác nhau như:
Toán học: Nghiên cứu về số chính phương giúp chúng ta hiểu sâu hơn về lý thuyết số.
Khoa học máy tính: Số chính phương được sử dụng trong các thuật toán và cấu trúc dữ liệu.
Kiến trúc: Số chính phương được ứng dụng trong thiết kế các công trình kiến trúc.
Tham khảo: Định lý pytago
Một số ví dụ về số chính phương
|
Số
|
Bình phương
|
|
1
|
1
|
|
2
|
4
|
|
3
|
9
|
|
4
|
16
|
|
5
|
25
|
|
...
|
...
|
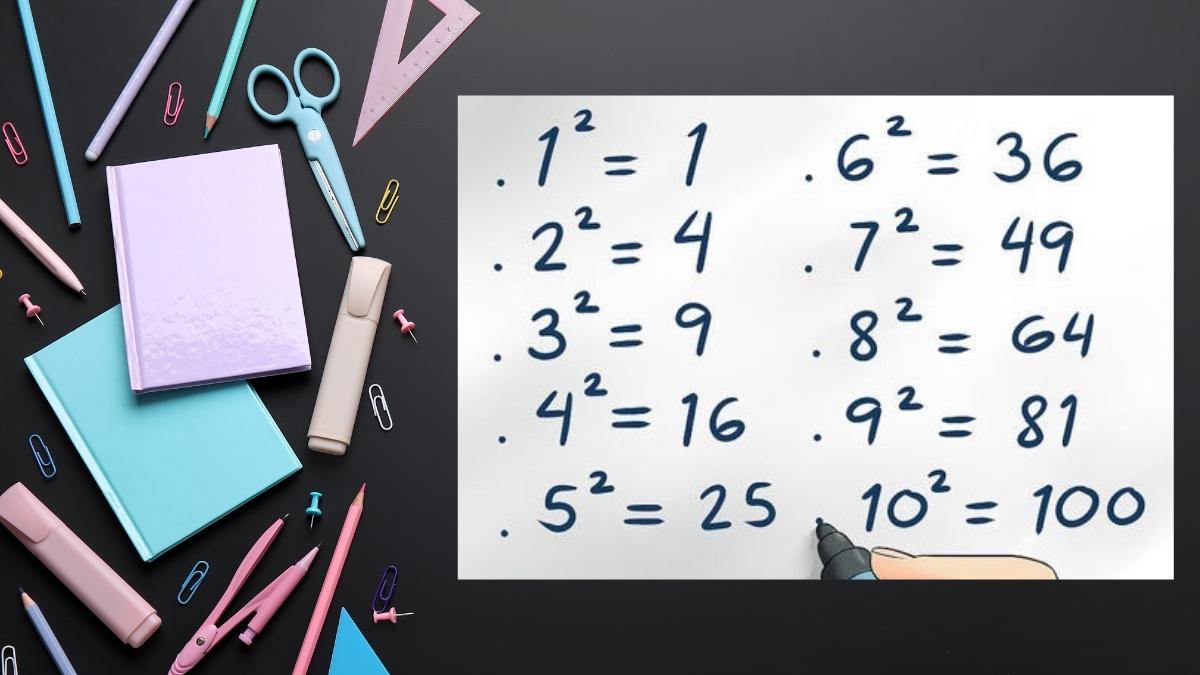
Số chính phươngTính chất của số chính phương
Số chính phương có nhiều tính chất thú vị, trong đó có một số tính chất đặc trưng sau:
Chữ số tận cùng: Số chính phương chỉ có thể có các chữ số tận cùng là 0, 1, 4, 5, 6 hoặc 9.
Phân tích ra thừa số nguyên tố: Các số mũ của các thừa số nguyên tố trong phân tích của một số chính phương luôn là số chẵn.
Tổng các chữ số: Không có quy luật chung để xác định một số có phải là số chính phương hay không chỉ dựa vào tổng các chữ số của nó.
Hình học: Số chính phương biểu diễn diện tích của một hình vuông có cạnh là số tự nhiên.
Cách nhận biết số chính phương
Tính căn bậc hai
Cách đơn giản nhất là tính căn bậc hai của số đó. Nếu kết quả là một số tự nhiên thì số đó là số chính phương.
Phân tích ra thừa số nguyên tố
Phân tích số đó ra thừa số nguyên tố. Nếu tất cả các số mũ đều là số chẵn thì đó là số chính phương.
Quan sát chữ số tận cùng
Kiểm tra chữ số tận cùng của số đó. Nếu không phải là một trong các chữ số 0, 1, 4, 5, 6 hoặc 9 thì chắc chắn đó không phải là số chính phương.
Sử dụng máy tính
Nhiều máy tính bỏ túi hoặc phần mềm tính toán có chức năng kiểm tra số chính phương.
Ví dụ
Số 144 có phải là số chính phương không?
Ta có: √144 = 12
Vậy 144 là số chính phương.
Số 153 có phải là số chính phương không?
Ta có: √153 ≈ 12,36
Vậy 153 không phải là số chính phương.

Số chính phươngSố nguyên tố là những số tự nhiên lớn hơn 1, chỉ có hai ước số là 1 và chính nó. Nói cách khác, đó là những số tự nhiên không thể chia hết cho bất kỳ số nào khác ngoài 1 và chính nó. Bạn có thể hình dung số nguyên tố như những viên gạch cơ bản, từ đó xây dựng nên tất cả các số tự nhiên khác.
Ví dụ: Các số 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 ... là số nguyên tố.
Vì sao số nguyên tố lại quan trọng?
Nền tảng của số học: Số nguyên tố là nền tảng để hiểu về các số tự nhiên khác.
Mã hóa: Số nguyên tố được sử dụng rộng rãi trong các thuật toán mã hóa để bảo mật thông tin.
Kiểm tra tính nguyên tố: Là một vấn đề toán học khó và có nhiều ứng dụng trong khoa học máy tính.
Số nguyên tố và số chính phương: Điểm khác biệt
|
Đặc điểm
|
Số nguyên tố
|
Số chính phương
|
|
Định nghĩa
|
Số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó
|
Bình phương của một số tự nhiên.
|
|
Ví dụ
|
2, 3, 5, 7, 11, ...
|
1, 4, 9, 16, 25, ...
|
|
Ước số
|
Chỉ có 2 ước số
|
Có thể có nhiều hơn 2 ước số.
|
|
Căn bậc hai
|
Không phải số tự nhiên (trừ số 1)
|
Luôn là số tự nhiên.
|
|
Chữ số tận cùng
|
Không có quy luật nhất định.
|
Luôn luôn là các số 0, 1, 4, 5, 6, 9.
|
Sự liên kết giữa số nguyên tố và số chính phương
Mặc dù khác nhau về định nghĩa và tính chất, nhưng số nguyên tố và số chính phương vẫn có mối liên hệ mật thiết với nhau. Ví dụ:
Định lý cơ bản của số học: Mọi số tự nhiên lớn hơn 1 đều có thể phân tích duy nhất thành tích của các số nguyên tố.
Số nguyên tố Fermat: Là những số nguyên tố có dạng 2^(2^n) + 1, chúng có liên quan đến việc tìm kiếm số chính phương hoàn hảo.
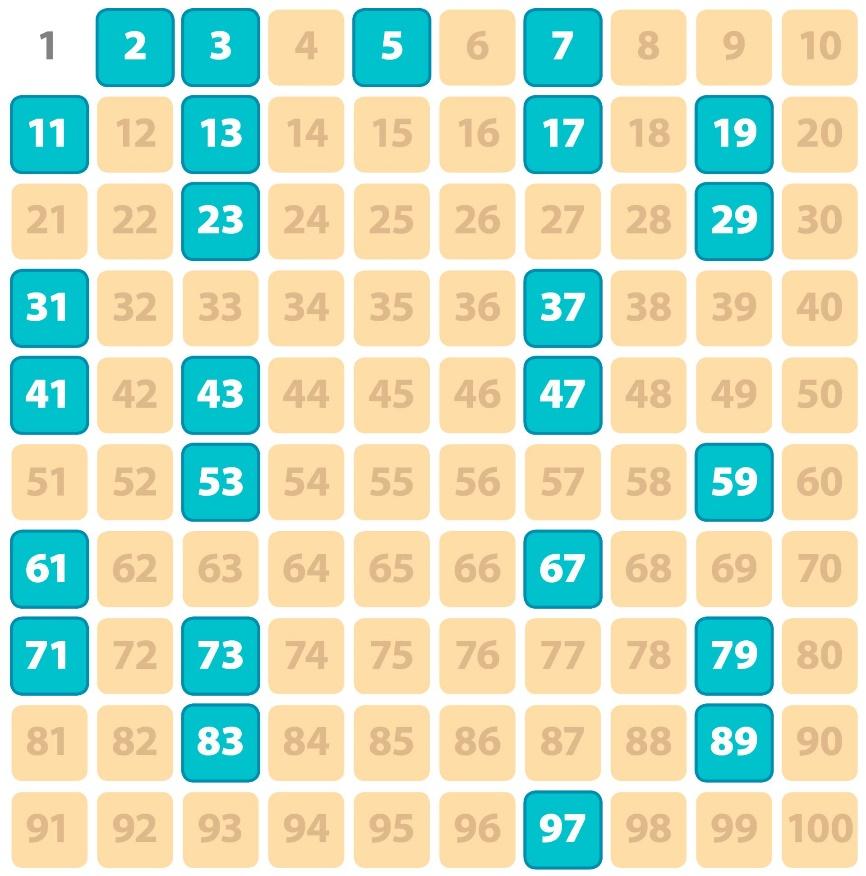
Số nguyên tốTìm số nguyên tố
Liệt kê các số nguyên tố trong một khoảng cho trước.
Kiểm tra xem một số có phải là số nguyên tố hay không.
Tìm các số nguyên tố thỏa mãn điều kiện cho trước (ví dụ: số nguyên tố có hai chữ số, số nguyên tố có tổng các chữ số bằng một số cho trước).
Tìm số chính phương
Kiểm tra xem một số có phải là số chính phương hay không.
Tìm các số chính phương trong một khoảng cho trước.
Tìm các số chính phương thỏa mãn điều kiện cho trước (ví dụ: số chính phương có bốn chữ số, số chính phương có tổng các chữ số bằng một số cho trước).
Bài toán kết hợp số nguyên tố và số chính phương
Tìm số tự nhiên nhỏ nhất vừa là số nguyên tố vừa là số chính phương.
Tìm các cặp số (a, b) thỏa mãn cả a và b đều là số nguyên tố và a + b cũng là số chính phương.
Ví dụ bài tập:
Tìm tất cả các số nguyên tố có hai chữ số mà khi đảo ngược các chữ số thì vẫn được một số nguyên tố.
Chứng minh rằng tổng của hai số chính phương liên tiếp không thể là số chính phương.
Tìm số tự nhiên n nhỏ nhất sao cho n^2 + 1 chia hết cho 5.
Trên đây là một số thông tin về số chính phương là gì, hi vọng các bạn sẽ có cho mình thông tin hữu ích.