Công thức cấp số cộng
Cấp số cộng là một khái niệm cơ bản nhưng vô cùng quan trọng trong toán học, đặc biệt là trong lĩnh vực đại số. Nó xuất hiện rất nhiều trong các bài toán thực tế, từ những vấn đề đơn giản như tính toán số tiền tiết kiệm hàng tháng đến những bài toán phức tạp hơn trong các ngành khoa học tự nhiên.
Cấp số cộng là gì?
Nói một cách đơn giản, cấp số cộng là một dãy số có tính chất đặc biệt: hiệu giữa hai số hạng liên tiếp luôn bằng một số không đổi. Số không đổi này được gọi là công sai.
Ví dụ: Dãy số 2, 5, 8, 11, 14,... là một cấp số cộng với công sai d = 3.
Các yếu tố cơ bản của cấp số cộng
Số hạng đầu: Là số hạng đứng đầu tiên trong dãy số, thường được ký hiệu là u1.
Công sai: Là hiệu số giữa hai số hạng liên tiếp, ký hiệu là d.
Số hạng tổng quát: Là công thức cho phép tính bất kỳ số hạng nào trong dãy số dựa vào số thứ tự của nó và các yếu tố đã biết (số hạng đầu và công sai).
Công thức cấp số cộng là:
un = u1 + (n - 1)d Trong đó:
un là số hạng thứ n
u1 là số hạng đầu
n là thứ tự của số hạng
d là công sai
Tổng n số hạng đầu: Công thức tính tổng n số hạng đầu của cấp số cộng là:
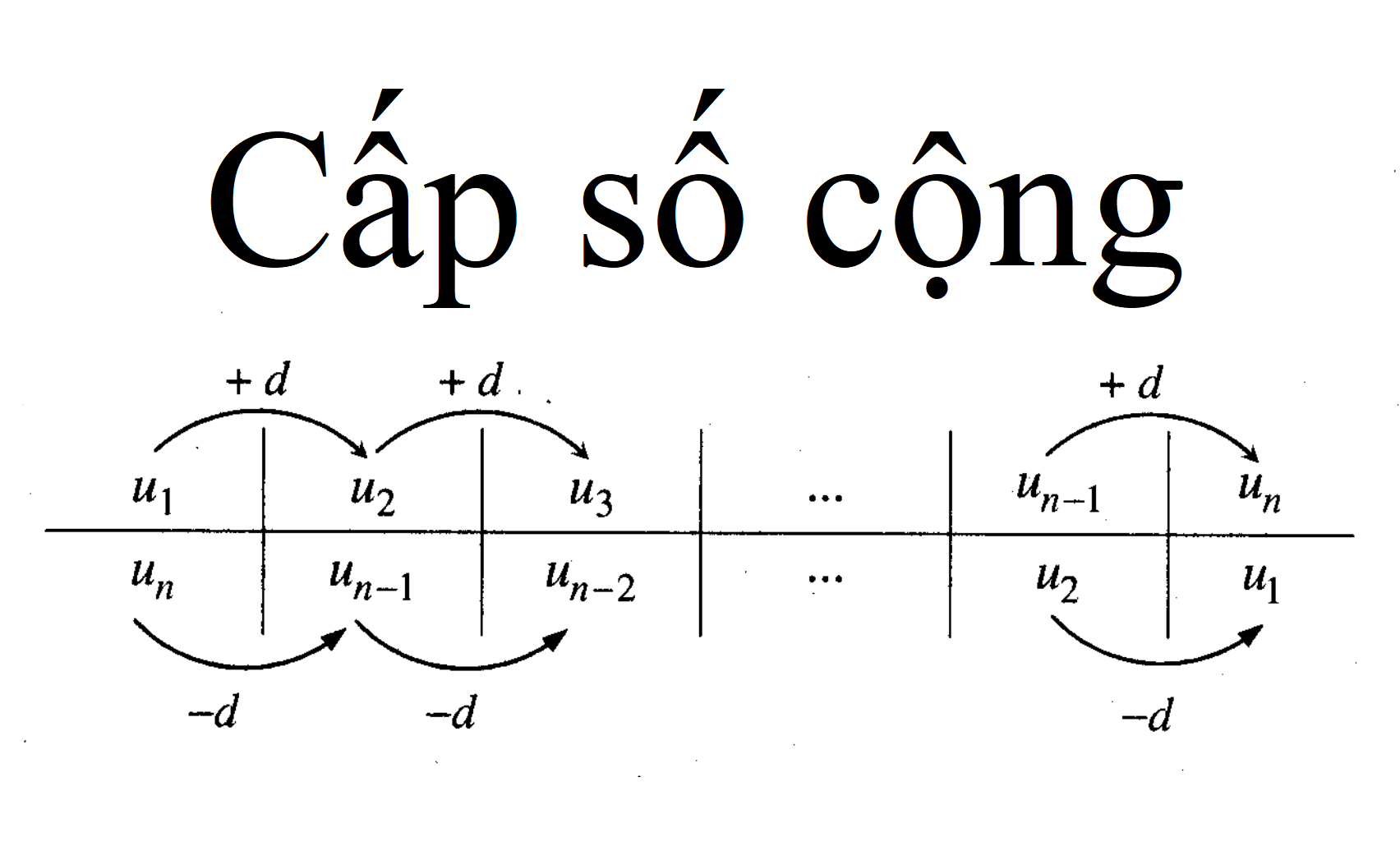
Cấp số cộngCấp số nhân là gì?
Cấp số nhân là một dãy số có tính chất đặc biệt: kể từ số hạng thứ hai, mỗi số hạng đều bằng tích của số hạng đứng ngay trước đó với một số không đổi. Số không đổi này được gọi là công bội của cấp số nhân.
Ví dụ: Dãy số 2, 4, 8, 16, ... là một cấp số nhân với công bội q = 2. Ta thấy mỗi số hạng sau bằng số hạng trước nhân với 2.
Công thức tổng quát
Để mô tả một cấp số nhân một cách tổng quát, ta sử dụng công thức sau:
uₙ = u₁.qⁿ⁻¹
Trong đó:
uₙ: Số hạng thứ n của cấp số nhân
u₁: Số hạng đầu tiên
q: Công bội
n: Vị trí của số hạng
Tính chất của cấp số nhân
Bình phương của mỗi số hạng (trừ số hạng đầu và cuối) bằng tích của hai số hạng đứng kề với nó.
Tích của ba số hạng liên tiếp luôn không đổi.
Ví dụ minh họa
Giả sử bạn gửi vào ngân hàng 10 triệu đồng với lãi suất 10%/năm. Nếu lãi được cộng vào vốn hàng năm, thì số tiền bạn có được sau mỗi năm sẽ tạo thành một cấp số nhân.
Năm thứ nhất: 10.000.000 x (1 + 10%) = 11.000.000 đồng
Năm thứ hai: 11.000.000 x (1 + 10%) = 12.100.000 đồng

Cấp số nhânChào bạn, rất vui được cùng bạn khám phá thế giới của cấp số cộng và cấp số nhân. Hai khái niệm này tưởng chừng chỉ xuất hiện trong những bài toán khô khan, nhưng thực tế chúng lại có vai trò vô cùng quan trọng trong cuộc sống hàng ngày.
Tại sao chúng ta cần học về công thức cấp số cộng và cấp số nhân?
Có thể bạn sẽ thắc mắc, học những thứ này để làm gì? Thực tế, cấp số cộng và cấp số nhân có rất nhiều ứng dụng trong cuộc sống, ví dụ như:
Tài chính: Tính lãi kép, tính giá trị hiện tại của một khoản tiền,...
Vật lý: Mô hình hóa các hiện tượng tự nhiên như dao động điều hòa, sự phân rã phóng xạ,...
Sinh học: Mô hình hóa sự tăng trưởng của quần thể, sự lây lan của dịch bệnh,...
Kinh tế: Dự báo xu hướng, phân tích thị trường,...
Các công thức quan trọng
Để giải quyết các bài toán liên quan đến cấp số cộng và cấp số nhân, chúng ta cần nắm vững một số công thức cơ bản sau:
Cấp số cộng:
Số hạng tổng quát: Un = U1 + (n-1)d
Tổng n số hạng đầu: Sn = n/2[2U1 + (n-1)d]
Cấp số nhân:
Số hạng tổng quát: Un = U1.q^(n-1)
Tổng n số hạng đầu: Sn = U1.(1-q^n) / (1-q) (với q ≠ 1)

Cấp số cộng và cấp số nhânCác dạng bài tập thường gặp:
Khi làm các bài tập về cấp số cộng và cấp số nhân, bạn sẽ thường gặp các dạng bài sau:
Tìm số hạng tổng quát: Dựa vào các điều kiện cho trước, tìm công thức tính số hạng thứ n của cấp số.
Tìm số hạng cụ thể: Tìm giá trị của một số hạng nhất định trong cấp số.
Tìm công sai hoặc công bội: Tìm giá trị của công sai (cấp số cộng) hoặc công bội (cấp số nhân).
Tính tổng n số hạng đầu: Tính tổng của một dãy số hữu hạn các số hạng đầu tiên của cấp số.
Chứng minh một dãy số là cấp số cộng hoặc cấp số nhân: Áp dụng định nghĩa và tính chất để chứng minh.
Các bài toán liên quan đến cấp số cộng và cấp số nhân: Kết hợp với các kiến thức khác như hàm số, phương trình, bất phương trình,...
Mẹo nhỏ để giải bài tập hiệu quả:
Nắm vững lý thuyết: Hiểu rõ định nghĩa, công thức và các tính chất của cấp số cộng và cấp số nhân.
Phân tích đề bài: Đọc kỹ đề bài, xác định rõ những gì đã cho và những gì cần tìm.
Lập phương trình: Dựa vào các dữ kiện trong đề bài, lập các phương trình phù hợp.
Giải phương trình: Giải các phương trình để tìm ra kết quả.
Kiểm tra lại kết quả: Sau khi tìm được đáp án, hãy kiểm tra lại xem kết quả có hợp lý không.
Nguồn tài liệu tham khảo:
Để tìm thêm nhiều bài tập và lời giải chi tiết, bạn có thể tham khảo:
Sách giáo khoa toán học: Các bài tập trong sách giáo khoa sẽ giúp bạn làm quen với kiến thức cơ bản.
Sách bài tập toán: Cung cấp nhiều bài tập đa dạng và nâng cao.
Các trang web học toán trực tuyến: Có rất nhiều trang web cung cấp bài tập, video hướng dẫn và diễn đàn để bạn trao đổi với các bạn cùng học.
Trên đây là các thông tin về công thức cấp số cộng và cấp số nhân. Hi vọng các bạn đã có cho mình thông tin hữu ích.