Số chính phương là gì
Định nghĩa trong toán học về số chính phương là gì
Số chính phương, còn được gọi là số hình vuông hoặc số toàn phương, là một số tự nhiên có thể biểu diễn dưới dạng bình phương của một số nguyên. Khi ta có một số n được viết thành k nhân với k, hay k^2, thì n chính là số chính phương. Chẳng hạn, nếu n bằng 25, ta có thể thấy 25 bằng 5 nhân 5, nên 25 là một số chính phương.
Khái niệm này xuất phát từ hình học. Khi sắp xếp các ô vuông nhỏ thành một hình vuông hoàn chỉnh, tổng số ô luôn là một số chính phương. Ví dụ, nếu ta sắp xếp 9 ô thành hình 3 hàng 3 cột, con số 9 thể hiện rõ ý nghĩa của một số chính phương.
Ví dụ minh họa
Những số nhỏ thường gặp như 1, 4, 9, 16 hay 25 đều là số chính phương. Nếu lấy căn bậc hai của chúng, ta sẽ thu được kết quả là số nguyên. Ngược lại, nếu một số có căn bậc hai không nguyên, số đó chắc chắn không phải là số chính phương. Ví dụ, 50 có căn bậc hai bằng khoảng 7, 07, nên 50 không phải số chính phương.
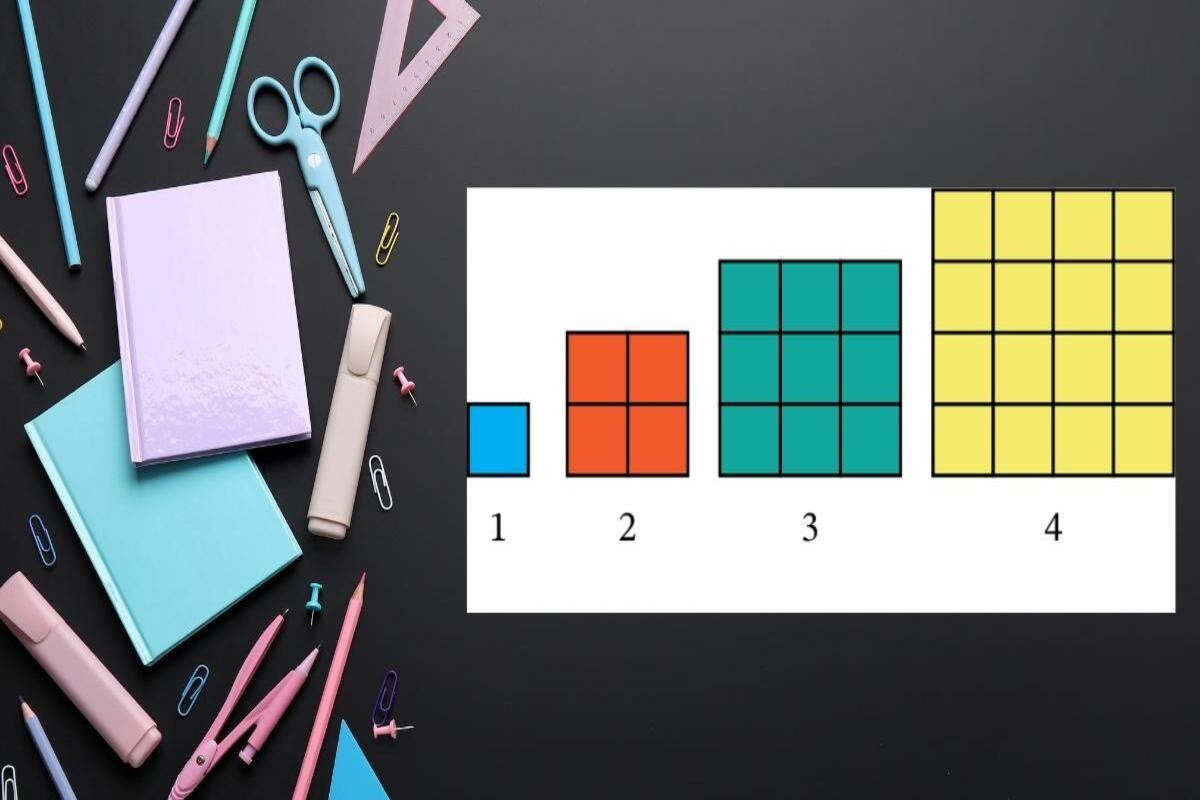 Số 9 là số chính phương vì có thể sắp xếp thành hình vuông hoàn chỉnh
Số 9 là số chính phương vì có thể sắp xếp thành hình vuông hoàn chỉnhCách nhận biết đơn giản
Một cách phổ biến để kiểm tra một số có phải số chính phương hay không là lấy căn bậc hai. Nếu kết quả là số nguyên, ta có thể khẳng định ngay đó là số chính phương. Ví dụ, căn bậc hai của 36 bằng đúng 6, chứng tỏ 36 là số chính phương.
Ngoài ra, số chính phương chỉ có thể kết thúc bằng 0, 1, 4, 5, 6 hoặc 9. Nếu một số tận cùng bằng 2, 3, 7 hoặc 8 thì chắc chắn không thể là số chính phương. Chẳng hạn, 144 kết thúc bằng 4 nên có khả năng là số chính phương, và đúng như vậy, 144 bằng 12 bình phương. Trong khi đó, 127 kết thúc bằng 7 nên chắc chắn không thể là số chính phương.
Liên hệ với phân tích thừa số nguyên tố
Một tính chất quan trọng khác là khi phân tích một số thành thừa số nguyên tố, số đó chỉ là số chính phương nếu tất cả số mũ trong phân tích đều là số chẵn. Lấy ví dụ với 36, khi phân tích ta được 36 bằng 2^2 \times 3^2. Cả hai số mũ đều là chẵn, vì vậy 36 là số chính phương. Ngược lại, 72 bằng 2^3 \times 3^2, trong đó số mũ 3 là số lẻ, nên 72 không phải là số chính phương.
 Một số là chính phương nếu căn bậc hai của nó là số nguyên
Một số là chính phương nếu căn bậc hai của nó là số nguyênƯớc số và số chính phương
Điểm thú vị nằm ở chỗ mọi số chính phương đều có số lượng ước là một số lẻ. Chẳng hạn, 16 là 4^2 và có các ước 1, 2, 4, 8 và 16. Tổng cộng có 5 ước, đây là một số lẻ. Trong khi đó, 18 vốn không phải số chính phương lại có 6 ước, tức số chẵn. Tính chất này thường được sử dụng trong các bài toán số học liên quan đến ước và bội.
Khoảng cách giữa hai số chính phương liên tiếp
Khoảng cách giữa hai số chính phương liên tiếp k^2 và (k+1)^2 luôn bằng 2k+1. Nếu ta lấy 25 là 5^2 và 36 là 6^2, thì hiệu của chúng bằng 11, đúng bằng 2 x 5+1. Với 100 là 10^2 và 121 là 11^2, hiệu bằng 21, tương ứng với 2 \times 10+1. Điều này cho thấy số chính phương không chỉ thú vị ở định nghĩa mà còn mang nhiều tính quy luật.
Phân bố trong dãy số tự nhiên
Nếu nhìn vào dãy số tự nhiên, số chính phương xuất hiện thưa thớt. Khi dãy số càng lớn, tỉ lệ số chính phương so với toàn bộ dãy càng nhỏ. Chẳng hạn trong khoảng từ 1 đến 100 có 10 số chính phương, nhưng trong khoảng từ 1 đến 10.000 lại chỉ có 100 số chính phương. Điều này chứng minh rằng xác suất chọn ngẫu nhiên được một số chính phương trong tập hợp số tự nhiên rất thấp.
 Số chính phương
Số chính phươngTrong học tập và toán học cơ bản
Khái niệm số chính phương được sử dụng rộng rãi trong chương trình toán từ tiểu học đến trung học phổ thông. Nó xuất hiện trong phần căn bậc hai, phương trình bậc hai và nhiều dạng bài chứng minh số học. Việc hiểu rõ số chính phương giúp học sinh dễ dàng nhận diện và giải quyết các bài toán liên quan.
Trong hình học trực quan
Diện tích của một hình vuông chính là bình phương của độ dài cạnh. Điều này có nghĩa mọi diện tích của hình vuông đều là số chính phương. Nếu một cạnh dài 7 đơn vị, diện tích sẽ là 49 đơn vị vuông, và 49 chính là số chính phương. Ứng dụng này gắn liền giữa số học và hình học, tạo sự trực quan sinh động cho người học.
Trong đời sống thường ngày
Số chính phương xuất hiện trong nhiều hoạt động thực tế. Khi sắp xếp một đội hình hình vuông, người ta thường chọn số lượng người là một số chính phương, chẳng hạn 16 người để thành hàng 4 \times 4. Khi thiết kế công viên hay vườn hoa, người ta có thể bố trí 49 cây cảnh thành hình 7 x 7. Tất cả đều thể hiện sự ứng dụng gần gũi của số chính phương.
Trong công nghệ và lập trình
Trong lĩnh vực lập trình, số chính phương có ý nghĩa khi xử lý dữ liệu dạng ma trận hoặc hình ảnh. Một bức ảnh kích thước 256 \times 256 pixel có tổng số điểm ảnh là 65.536, và con số này chính là bình phương của 256. Những đặc điểm này giúp việc xử lý hình ảnh trở nên thuận tiện và đồng bộ hơn.
Qua bài viết, bạn đã có cái nhìn toàn diện về câu hỏi số chính phương là gì. Đây là những con số có thể biểu diễn thành bình phương của một số nguyên, mang nhiều tính chất đặc biệt và ứng dụng rộng rãi trong toán học cũng như trong đời sống thực tế. Từ việc tính diện tích hình vuông, sắp xếp đội hình cho đến xử lý dữ liệu trong công nghệ, số chính phương luôn hiện diện như một khái niệm cơ bản nhưng quan trọng.