Công thức cấp số cộng
Cấp số cộng (CSC) là một dãy số trong đó mỗi số hạng (từ số hạng thứ hai trở đi) bằng số hạng trước nó cộng với một số không đổi.
Số không đổi này được gọi là công sai, ký hiệu là d.
Dãy số được gọi là dãy số cấp số cộng nếu thỏa mãn:
a_(n+1) - a_n=d với mọi n ≥ 1
Trong đó:
a_n là số hạng thứ n của dãy,
d là công sai (có thể âm, dương hoặc bằng 0).
Ví dụ:
Dãy số 2, 5, 8, 11, 14 là một cấp số cộng vì:
5 - 2=3, 8 - 5=3, 11 - 8=3, 14 - 11=3
=> Công sai d=3
Dãy số 10, 7, 4, 1, -2 cũng là cấp số cộng với công sai d=-3.
💡 Lưu ý:
Cấp số cộng có thể tăng dần (d > 0), giảm dần (d < 0) hoặc bằng nhau (d=0).
Đây là nền tảng để tính số hạng bất kỳ và tổng n số hạng đầu tiên trong dãy số.

Định nghĩa về cấp số cộngCông thức tính số hạng tổng quát
Số hạng thứ n của cấp số cộng:
a_n=a_1+(n - 1) × d
Trong đó:
a_n là số hạng thứ n,
a_1 là số hạng đầu tiên,
d là công sai,
n là vị trí số hạng.
Công thức tính tổng n số hạng đầu tiên
Tổng S_n của n số hạng đầu tiên:
S_n=n/2 × (a_1 + a_n)
Hoặc thay a_n bằng công thức số hạng:
S_n=n/2 × [2 × a_1+(n - 1) × d]
Trong đó:
S_n là tổng n số hạng đầu tiên,
a_1 là số hạng đầu tiên,
d là công sai,
n là số lượng số hạng.

Công thức về cấp số cộng đầy đủ Công thức tìm công sai
Nếu biết hai số hạng a_m và a_n trong dãy:
d=(a_n - a_m) / (n - m)
💡 Lưu ý:
Các công thức này áp dụng cho mọi cấp số cộng, bất kể tăng dần, giảm dần hay công sai bằng 0.
Đây là nền tảng để giải tất cả bài tập về số hạng, tổng và công sai.
Công thức tổng cấp số cộng
Tổng S_n của n số hạng đầu tiên trong cấp số cộng:
S_n=n/2 × (a_1 + a_n)
Trong đó:
a_1 là số hạng đầu tiên,
a_n là số hạng thứ n,
n là số lượng số hạng.
Chứng minh công thức
Giả sử dãy số cấp số cộng là:
a_1, a_2, a_3, ..., a_n
Theo định nghĩa, mỗi số hạng cách nhau công sai d:
a_2=a_1+d
a_3=a_1+2d
...
a_n=a_1+(n-1)d
Tổng S_n có thể viết như sau:
S_n=a_1+a_2+a_3+...+a_n
Bước 1: Viết tổng theo thứ tự thuận và nghịch
S_n=a_1+a_2+a_3+...+a_(n-1)+a_n
S_n=a_n+a_(n-1)+...+a_2+a_1
Bước 2: Cộng hai biểu thức lại
2 × S_n=(a_1 + a_n)+(a_2 + a_(n-1))+...+(a_n + a_1)
Mỗi cặp (a_k + a_(n-k+1))=a_1+a_n và có n cặp như vậy.
2 × S_n=n × (a_1 + a_n)
Bước 3: Chia cho 2
S_n=n/2 × (a_1 + a_n)
✅ Như vậy, công thức tổng cấp số cộng được chứng minh.
💡 Lưu ý:
Phương pháp này dùng kỹ thuật viết tổng thuận – nghịch rất trực quan.
Khi a_n chưa biết, có thể thay bằng a_n=a_1+(n-1)d để có công thức:
S_n=n/2 × [2a_1+(n-1)d]
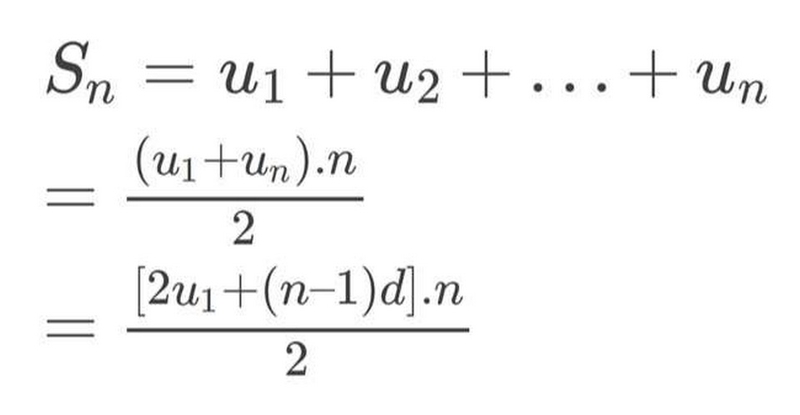
Ví dụ minh họa áp dụng công thức về cấp số cộng?Ví dụ 1: Tính số hạng thứ n
Một cấp số cộng có số hạng đầu tiên a_1=3 và công sai d=5. Tìm số hạng thứ 10 (a_10).
Công thức số hạng thứ n:
a_n=a_1+(n - 1) × d
Áp dụng:
a_10=3+(10 - 1) × 5
a_10=3+9 × 5
a_10=3+45
a_10=48
✅ Số hạng thứ 10 là 48.
Ví dụ 2: Tính tổng n số hạng đầu tiên
Cấp số cộng 2, 5, 8, 11, ... có số hạng đầu a_1=2 và công sai d=3. Tính tổng 20 số hạng đầu tiên.
Công thức tổng n số hạng đầu:
S_n=n/2 × [2a_1+(n - 1)d]
Áp dụng:
S_20=20/2 × [2× 2+(20 - 1)× 3]
S_20=10 × [4+19× 3]
S_20=10 × [4+57]
S_20=10 × 61
S_20=610
✅ Tổng 20 số hạng đầu tiên là 610.
Ví dụ 3: Tìm công sai khi biết hai số hạng
Một cấp số cộng có số hạng thứ 4 là 20 và số hạng thứ 10 là 38. Tìm công sai d.
Công thức tìm công sai:
d=(a_n - a_m) / (n - m)
Áp dụng:
d=(38 - 20) / (10 - 4)
d=18 / 6
d=3
✅ Công sai của dãy là 3.
💡 Lưu ý:
Các công thức áp dụng cho mọi cấp số cộng, bất kể tăng dần, giảm dần hay công sai âm.
Việc chia thành các ví dụ tính số hạng, tổng và công sai giúp dễ hiểu và vận dụng linh hoạt.
Ứng dụng của cấp số cộng trong toán học
Tính số hạng bất kỳ trong dãy số:
Cấp số cộng giúp xác định số hạng thứ n bằng công thức:
a_n=a_1+(n - 1)d
Ví dụ: Trong dãy số 2, 5, 8, 11, … , số hạng thứ 20 có thể tính nhanh mà không cần liệt kê tất cả các số hạng.
Tính tổng n số hạng đầu tiên:
Công thức tổng n số hạng đầu tiên:
S_n=n/2 × [2a_1+(n - 1)d]
Ứng dụng trong các bài toán tổng các số liên tiếp, tổng các dãy số trong đại số hoặc bài toán thực tế.
Xác định công sai và số hạng:
Khi biết hai số hạng bất kỳ, có thể tìm công sai bằng công thức:
d=(a_n - a_m)/(n - m)
Điều này giúp giải quyết nhanh các bài toán yêu cầu tìm quy luật của dãy số.
Nền tảng để nghiên cứu dãy số khác:
Cấp số cộng là cơ sở để hiểu cấp số nhân, dãy Fibonacci, hoặc các dãy số trong hình học số học, lý thuyết tổ hợp, thống kê.
Ứng dụng của cấp số cộng trong đời sống thực tế
Tài chính và kế hoạch tiết kiệm:
Nếu mỗi tháng bạn gửi tiết kiệm tăng thêm một số tiền cố định so với tháng trước, tổng số tiền sau n tháng được tính bằng công thức tổng cấp số cộng.
Ví dụ: Gửi 1 triệu VNĐ tháng đầu, mỗi tháng tăng thêm 100.000 VNĐ, tổng tiền sau 12 tháng có thể tính nhanh mà không cần cộng từng tháng.
Xây dựng và kiến trúc:
Xác định chiều cao cầu thang, khoảng cách cột, dầm theo quy luật đều nhau.
Tính tổng chiều cao nhiều tầng hoặc khoảng cách gia tăng/giảm dần theo một công sai cố định, giúp thiết kế chính xác và tiết kiệm thời gian.
Kỹ thuật và sản xuất:
Lập kế hoạch sản xuất tăng dần theo ngày hoặc tuần.
Bố trí các chi tiết, khoảng cách các bộ phận trong dây chuyền sản xuất theo quy luật tăng dần để tối ưu không gian và hiệu quả.
Lịch trình học tập hoặc công việc:
Sắp xếp thời gian giữa các buổi họp, luyện tập hoặc kiểm tra theo một khoảng thời gian đều hoặc tăng dần.
Giúp lên kế hoạch khoa học và dễ theo dõi tiến độ.
Các ứng dụng trong đời sống khác:
Tính số ghế, bậc thang, khoảng cách cây trồng, số lượng vật phẩm cần chuẩn bị khi tăng dần theo quy luật cố định.
Giúp lập kế hoạch nhanh chóng, chính xác và tiết kiệm công sức.
Trên đây chúng tôi đã giới thiệu định nghĩa, công thức, cách chứng minh và các ứng dụng của công thức cấp số cộng trong toán học và đời sống. Hy vọng bài viết sẽ giúp bạn nắm vững kiến thức, giải các bài tập dễ dàng và áp dụng hiệu quả trong thực tế.